Fibonaccin illuusio

Fibonaccin lukujonolla tarkoitetaan jonoa, jonka 1. ja 2. luku ovat ykkösiä, ja muut luvut saadaan laskemalla kaksi edellistä lukua yhteen. Se on saanut nimensä 1200 luvulla eläneen Fibonaccicsi kutsutun Leonardo Pisalaisen mukaan. Fibonaccin luvuista käytetään yleensä merkintää, jossa n:s luku on F_n. Jonoon katsotaan joskus kuuluvaksi myös luku F₀=0. Fibonaccin jonoon kuuluvista luvuista käytetään yhteisnimitystä Fibonaccin luvut. Lukujonoja, jotka muodostetaan samoin kuin Fibonaccin jono, paitsi että kaksi ensimmäistä jäsentä voivat olla mitä tahansa positiivisia kokonaislukuja kutsutaan yleistetyiksi Fibonaccin jonoiksi.

Fibonaccin lukuihin liityy seuraavia mielenkiintoisia ominaisuuksia

1. F_n+1²=F_nF_n+2+(-1)ⁿ,n³1

2. F_2n+1=F_n²F_n+1²

3. F_n+2²-F_n+1²=F_nF_n+3

6. Joka n:s Fibonaccin luku on jaollinen F_n:llä.

7. syt(F_n,F_n+1)=1

8. F_n/F_n+1lähenee kultaista leikkausta kun n lähenee ääretöntä.

Ominaisuuteen 1 liittyy seuraava kuuluisa illuusio:

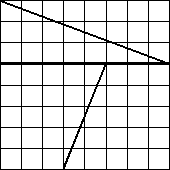
Leikataan ruutupaperista shakkilaudan kokoinen, eli 8*8=64 ruudun neliö, ja paloitellaan se seuraavan kuvan osoittamalla tavalla:

Palaset irroittaa toisistaan voidaan järjestää uudestaan siten, että ne muodostavat seuraavan laisen kuvion:

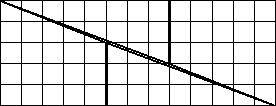
Kuvion sivut ovat 5 ja 13 ruutua, joten sen pinta-alaksi saadaan 65 ruutua! Jomman kumman kuvion ala on siis laskettu väärin. Jälkimmäinen kuvio ei itse asiassa olekaan suorakaide. Sen keskellä on hyvin kapea suunnikkaan muotoinen aukko, jonka pinta-ala on 1. Tämän suunnikkaan kärkipisteet ovat myötäpäivään A, C, D ja B. Virheen voi havaita jo siitäkin, että kappaleiden vinojen sivuje kulmakertoimet ovat erisuuruiset (-3/8 ja -5/2).

Virheen vaikea havaittavuus perustuu siihen, että 5, 8 ja 13 ovat kolme peräkkäistä Fibonaccin lukua, joista keskimmäisen neliö poikkeaa ominaisuuden 1 mukaan yhdellä sen kummallakin puolella sijaitsevien lukujen tulosta. Poikkeaman suunta riippuu siitä, onko keskimmäisen luvun järjestysluku parillinen vai pariton, ja siksi illuusio toteutuukin parhaiten parillista astetta olevilla Fibonaccin luvuilla. Illuusio tulee sitä vakuuttavammaksi, mitä suurempia lukuja käytetään. Esimerkiksi kun valitaan luvut 13, 21 ja 34, saadaan "pinta-aloiksi" 442 ja 441. Suunnikkaan leveydeksi tulee tällöin vain 0,4.

Sampo Tiensuu