Siiven tekniikkaa

Kuva 1: DeHavilland Tiger Moth - lentokone kaksine siipineen.

Lentokoneen siiven toimintaperiaate selitetään usein virheellisesti. Jopa joissakin lentokoulujen oppikirjoissa esitetään yksinomaan Bernoullin periaatteeseen nojaava malli siiven toiminnalle. Tämän mallin mukaan siipiprofiili tuottaa nostovoimaa, koska siiven yläpinnalla nopeammin kulkeva ilmavirta aiheuttaa alipaineen, joka imee siipeä ylöspäin. Ilmavirran nopeutuminen taas selitetään sillä, että hiukkasten täytyy taittaa siiven yläpinnalla pidempi matka kuin alapinnalla, jotta ne kohtaisivat takareunalla. Ei ole kuitenkaan mitään fysikaalista perustetta sille, että samojen molekyylien olisi oltava vierekkäin sekä ennen että jälkeen siiven. Tämän lisäksi mallin voi kumota aivan käytännön esimerkeillä: Monilla lentokoneilla voidaan lentää ylösalaisin, jolloin ylempänä pintana toimii lyhyempi alapinta. Todistettavasti myös monien liidokkien levysiipi tuottaa nostetta, vaikka siiven pintojen välillä ei ole pituuseroa. Tarvitaan siis jokin muu teoria selittämään siiven toimintaa.

Siipiteoriaa

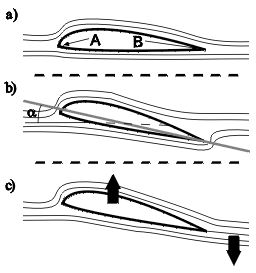Kuva 2: Ilmavirtaus siiven ympärillä eri kohtauskulmilla. a) kohtauskulma nolla, ei nostetta. A = etumainen patopiste, B = takimainen patopiste. b) kohtauskulmaa kasvatettu, mutta massattoman ideaalinesteen virtaus (ei kitkaa eikä inertiaa), a = kohtauskulma. c) kohtauskulmaa kasvatettu, ilmaan kohdistuu voima alas, siipeen voima ylös.

Siiven nostovoiman kannalta ratkaisevan tärkeä tekijä on siiven ns. kohtauskulma eli kulma, jossa siipi kohtaa vapaan ilmavirtauksen. Edetessään siipi jakaa ilmamassan kahteen osaan ns. etumaisessa patopisteessä. Vastaavasti siiven takaosassa on takimmainen patopiste (ks. kuva 1a). Jos siipi liikkuisi viskoosittomassa ja massattomassa ideaalinesteessä, patopisteet siirtyisivät kohtauskulman kasvaessa siiven pinnalla vapaan virtauksen mukaisiksi. Tämä tarkoittaa siis sitä, että etumainen piste siirtyy siiven alapinnalle ja takimmainen yläpinnalle (ks. kuva 1b). Niin sanotun Kutta-ehdon mukaan ilma kuitenkin pyrkii irtautumaan pinnalta mahdollisimman ”siististi”. Mikäli takimmainen patopiste olisi yläpinnalla, alapuolisen ilman täytyisi tehdä jyrkkä mutka siiven jättöreunan kohdalla päästäkseen patopisteeseen. Patopiste siis pysyy jättöreunalla, kun oletetaan, ettei kohtauskulmaa kasvateta liikaa.

Patopisteen siirtyminen alaspäin aiheuttaa muutoksen ilmamassan painejakaumaan ja Bernoullin lain mukaisesti nopeusjakaumaan, sillä matalampi painehan aiheuttaa suuremman nopeuden ja päinvastoin. Nopeusjakaumaa mallintaa suure nimeltä sirkulaatio. Tämä määritetään asettamalla siipiprofiilin ympärille sulkeutuva käyrä, jota pitkin ilman nopeusvektoreiden tangentiaalikomponentit integroidaan. Kun käyrää kuljetaan myötäpäivään, ovat vektorit siiven yläpuolella positiivisia, mutta alapuolella negatiivisia, koska virtauksen nopeus on vastakkainen käyrän kiertosuuntaan nähden. Kun siipi ei tuota nostovoimaa, kumoavat nopeusvektorit toisensa ja sirkulaatio on nolla. Patopisteen siirtyessä taakse- ja alaspäin sirkulaatio eroaa nollasta, sillä ilmamassan nopeusvektorien oikealle-alas-komponentit pitenevät ja vastakkaissuuntaiset vastaavasti lyhenevät. Sirkulaatio voidaan matemaattisesti laskea kaavalla:

missä Γ on sirkulaatio, v nopeuksien käyrän suhteen tangentiaalinen komponentti ja ds käyrän viivaelementti eli differentiaali. tarkoittaa integrointia suljettua käyrää pitkin.

Siipi siis pakottaa ilman takanaan alaspäin (ks. kuva 1c). Newtonin toisen lain mukaan voimalla on aina yhtä suuri mutta vastakkaissuuntainen vastavoima. Siipi kohdistaa ilmamassaan voiman, joka lisää sen liikemäärän alaspäin suuntautuvaa komponenttia. Tällöin siipeen itseensä kohdistuu vastavoima ylöspäin. Tämä voima on siis se, jota kutsumme siiven kohdalla nostovoimaksi. Sirkulaation avulla nostovoima voidaan laskea kaavalla:

missä ρ on ilman tiheys ja s siiven pituus. Sirkulaatio on kuitenkin todellisuudessa hankala määrittää. Siksi onkin kehitetty menetelmiä, joiden avulla nostovoima voidaan laskea kokeellisten tulosten perusteella.

Insinöörilaskentaa

Lentokoneen siipiä ei yleensä suunnitella alusta asti, sillä sirkulaation yms. fysikaalisten suureiden laskeminen on hyvin vaikeaa. Siivelle voidaan kokeellisesti määrittää ns. nostovoimakerroin kohtauskulman funktiona. Tämän kertoimen avulla nostovoima voidaan laskea kaavalla:

missä C_L on nostovoimakerroin ja A siiven pinta-ala. Kertoimia on määritetty valmiiksi lukuisille siipiprofiileille, joiden tiedot on julkaistu taulukkokirjoissa.

Kärkipyörteet

Siiven kulkiessa ilmojen halki sen yläpuolelle muodostuu alipaine. Ala- ja yläpuolen välille syntyvä paine-ero aiheuttaa ilmiön, jota kutsutaan kärkipyörteiksi. Siiven alapuolen ylipaine pyrkii tasoittumaan, mikä tapahtuu siiven kärkien kautta. Kärjissä vapaata virtausta vastaan kohtisuora eli siiven suuntainen ilmavirtaus kääntyy siiven yläpuolelle, mikä näkyy pyörteilynä siiven jäljessä. Tämä taas on erityisesti ilmailussa merkittävää, sillä suurien lentokoneiden tuottama noste aiheuttaa suuret paine-erot ja sitä kautta suuret pyörteet, jotka saattavat aiheuttaa vaaratilanteita pienemmille lentokoneille.

Eräs pyörteistä aiheutuva ilmiö on ns. indusoitu vastus. Kärkien kautta vuotavan paineen ansiosta äärellisen pitkän siiven hyötysuhde ei ole 100%. Osa energiasta karkaa kärkipyörteiden mukana indusoituna vastuksena. Siipeen kohdistuvat vastusvoimat voidaan laskea kaavalla:

missä C_D on nostovoimakerrointa vastaava kokeellisesti määritettävä vastuskerroin.

Sakkaus

Kuva 3: Tuulitunneli-insinööri työssään.

Toinen hyvin merkittävä ilmiö on sakkaus. Sakkausta esiintyy, kun kohtauskulmaa kasvatetaan niin paljon, että takimmainen patopiste ei enää pysy jättöreunalla. Tällöin ilmavirtaus siiven takaosassa irtoaa siiven pinnasta ja muuttuu turbulentiksi, jolloin siipi ei enää käännä virtausta eikä siis tuota nostovoimaa. Tämä lentotila on ymmärrettävästi turmiollinen, ja sen ilmenemistä pyritäänkin minimoimaan. Eräs keino on sakkausvaroitin, joka on yksinkertainen merkinantolaite. Mikäli paine siiven etureunassa laskee liiaksi, mikä tapahtuu kohtauskulman kasvaessa ja etumaisen patopisteen siirtyessä alaspäin, alkaa ilma virrata jonkinlaisen äänentuottolaitteen eli pillin tai painemittarin läpi, jolloin pilotti saa tiedon uhkaavasta vaarasta. Tämä tapahtuu ennen sakkausta, jolloin asennon korjaaminen on vielä mahdollista. Tällöin kohtauskulmaa tulee pienentää.

Sakkaus tapahtuu usein pienillä lentonopeuksilla, jolloin vaaditaan suurta kohtauskulmaa. Tämä on tilanne laskeuduttaessa, jolloin nostovoiman katoaminen olisi suorastaan letaalia. Siiven nostovoiman lisäämiseksi käytetäänkin poikkeuksetta laippoja eli laskusiivekkeitä, jotka kasvattavat siiven nostovoimakerrointa lisäämällä profiilin kaarevuutta. On kuitenkin huomattava, että sakkaus ei riipu suoraan ilmanopeudesta, vaan välillisesti kohtauskulman kautta. Hyvin suurellakin ilmanopeudella on mahdollista kasvattaa kohtauskulmaa liiaksi, jolloin tapahtuu ns. G-sakkaus. Monilla delta- eli kolmiosiipisillä lentokoneilla, kuten Concorde-yliäänimatkustajakoneella tai Draken-suihkuhävittäjällä, esiintyy myös ilmiö nimeltä supersakkaus. Tällöin koneen ohjainpinnat, jotka sijaitsevat siiven takaosassa, sakkaavat, eikä korjaaminen enää onnistu.

Jari Varje

Kirjallisuutta

[1] Wuori, Paul A.; Virtausmekaniikan perusteet. Otatieto, Espoo 1990.

[2] Denker, John S.; Momentum and Energy Near a Wing. http://www.monmouth.com/~jsd/fly/vortex/

[3] Haapanen, Erkki; Aerodynamiikka. Suomen Ilmailuliitto r.y., Lahti 1972.

[4] NASA; FoilSim II 1.4 beta. http://www.grc.nasa.gov/WWW/K- 12/airplane/foil2.html