Aritmetiikkaa geometrialla

Kun puhutaan geometrialla tapahtuvasta aritmetiikasta, tarkoitetaan tällöin tietenkin klassista harpilla ja viivaimella tapahtuvaa geometriaa. Jos janojen pituudet ajatellaan lukuina, niillä voidaan laskea geometrisesti. Yhteen- ja vähennyslasku on helppo toteuttaa siirtämällä janoja harpin avulla samalle suoralle. Kerto- ja jakolasku seuraavat yhdenmuotoisuudesta. Niistä on hyvä huomata se, että niitä ei voida laskea tietämättä yksikköjanaa, vaikka tämä onnistuikin yhteen- ja vähennyslaskussa. Näiden lisäksi voidaan kahden luvun tulon neliöjuuri laskea geometrisesti. Tämä perustuu siihen, että yhdenmuotoisuuden mukaan a/h = h/b, josta seuraa, että ab = vh. Yksittäisenkin luvun neliöjuuri voidaan laskea jos tiedetään yksikköjana.

Piirrettävät reaaliluvut

Oletetaan, että on annettu yksikköjana. Reaalilukua x sanotaan piirrettäväksi, mikäli tästä voidaan äärellisellä määrällä askelia muodostaa jana, jonka pituus on . Edellä esitetyistä laskutoimituksista huomaa, että ainakin kaikki rationaaliluvut ovat piirrettäviä. Tutkitaan, miten piirrettäviä lukuja voisi saada lisää, jos oletetaan, että alussa on käytössä rationaalikoordinaatit. Ensimmäisessä tapauksessa voidaan piirtää kaksi suoraa, ja katsoa missä ne leikkaavat. Tällöin syntyy ensimmäisen asteen yhtälö, jonka ratkaisemiseen yhteen- vähennys, kerto- ja jakolasku riittävät. Jos tutkitaan ympyrän ja suoran tai kahden ympyrän leikkauspistettä, saadaan toisen asteen yhtälö. Tällöin syntyy toisen asteen yhtälö, ja tarvitaan lisäksi myös neliöjuurta. Kun lopulta ollaan generoitu halutut kaksi pistettä, otetaan näiden etäisyys Pythagoraan lauseella. Tähänkin tarvitaan vain yhteen, kerto- ja jakolaskua. Tästä voidaan huomata, että itse asiassa edellä esitetyt viisi laskutoimitusta riittävät kaikkien piirrettävien lukujen kuvaamiseen. Ei ole kuitenkaan aivan helppoa päätellä lukua katsomalla voidaanko sitä esittää näiden operaatioiden avulla. Esimerkiksi monimutkaisen näköinen luku , joka näyttäisi mahdottomalta piirtää, onkin itse asiassa vain toisessa muodossa esitetty kultaisen leikkauksen suhde , joka on piirretävä1). Juuri tätä kultaista leikkaustahan käytettiin Seepian 3. numerossa säännöllisen viisikulmion muodostamiseen.

Kuntalaajennukset

Tämän kaltaisten lukujen käsittelyyn tarvitaan tietynlaisia työkaluja. Kunta on rakenne, jolle pätevät seuraavat, reaalilukujen aksioomia muistuttavat ehdot:

1. Kunnan F kaikille alkioille a ja b on määritelty a+b ja a×b siten, että a+bÎF ja a×bÎF

2. Kommutatiivisuus: a+b = b+a ja a×b = b×a

3. Assosiatiivisuus: (a+b)+c = b+(a+c)  ja (a×b)×c = b×(a×c)

4. Distributiivisuus: a×(b+c) = a×b+a×c ja (a+b)×a = a×c+b×c

5. On olemassa alkio (merkitään esimerkiksi 0) siten, että 0+x = x+0 = x kaikilla x.

6. Jokaiselle alkiolle x on olemassa käänteisalkio y yhteenlaskun suhteen siten, että x+y = y+x = 0.

7. On olemassa alkio (merkitään esimerkiksi 1) siten, että 1×x = x×1 = x kaikilla x

8. Jokaiselle alkiolle x ¹ 0 on olemassa käänteisalkio y kertolaskun suhteen siten, että x×y = y×x = 1. Kuntia ovat esimerkiksi 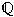, 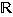ja .

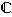Jos kunta E sisältää kunnan F, sanotaan kuntaa E kunnan F kuntalaajennukseksi. Otetaan esimerkiksi rationaalilukujen kunta, ja lisätään siihen . Lopputulos on kunta, jonka alkiot ovat muotoa , missä a,bÎ 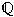. Tämä täyttää vaadittavat ominaisuudet. Jos otetaan vastaavalla tavalla mahdollisimman pieni kunta, joka sisältää , saadaan kunta , missä a,b,cÎ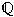. Tähän tarvittiin kolme komponenttia. Näiden komponenttien määrää kutsutaan kuntalaajennuksen asteeksi, ts. ensimmäisen kuntalaajennuksen aste oli 2 ja toisen 3. Piirrettävät reaaliluvut ovat selvästikin kunta, sillä ne täyttävät annetut vaatimukset. Jos lähdetään jostain piirrettävien reaalilukujen osakunnasta, kuten rationaaliluvuista, ovat plus-, miinus-, kerto-, ja jakolasku määriteltyjä kunnan sisällä. Laajennus voi siis tapahtua ainoastaan neliöjuuren ottamisen yhteydessä. Oletetaan, että laajennus tehdään siten, että halutaan pienin kunta, joka sisältää edellisen kunnan ja luvun . Tällöin on kaksi vaihtoehtoa. Jos kuuluu jo valmiiksi kuntaan, ei laajennusta tapahdu, joten tätä tapausta ei tarvitse ottaa huomioon. Jos se ei kuulu, tarvitaan lisää komponentteja. Jokaista vanhan kunnan komponenttia x kohden täytyy uudessa kunnassa olla kaksi komponenttia: x ja . Tämän takia laajennuksen aste kaksinkertaistuu aina täsmälleen silloin, kun joudutaan ottamaan ei-neliöllisen luvun neliöjuuri. Lopputulos on se, että jos otetaan pienin mahdollinen rationaalilukujen kuntalaajennus, johon x sisältyy, niin x on piirrettävä jos ja vain jos kuntalaajennuksen aste on kakkosen potenssi. Yksi kuntalaajennusten teorian perustuloksista on se, että jos otetaan pienin kunta, joka sisältää jonkin tietyn jaottoman kolmannen asteen polynomin minkä tahansa juuren, on tämän kunnan laajennuksen aste rationaalilukujen yli 3. Koska 3 ei ole kakkosen potenssi, saadaan sellainen käyttökelpoinen tulos, että jos on olemassa kolmannen asteen yhtälö, jolla ei ole rationaaliratkaisuja, ei sen mitään juurta voida piirtää harpilla ja viivaimella.  Lähdettäessä rationaaliluvuista laajennus voi syntyä neliöjuuren ottamisen yhteydessä. Tämä tuplaa kuntalaajennuksen asteen. Lopputulos on se, että jos otetaan pienin mahdollinen rationaalilukujen kuntalaajennus, johon x sisältyy, niin x on piirrettävä jos ja vain jos kuntalaajennuksen aste on kakkosen potenssi. Tästä saadaan sellainen käyttökelpoinen tulos, että jos kolmannen asteen rationaalikertoimisella yhtälöllä ei ole rationaalijuuria, sen mikään juuri ei ole piirrettävä.

Klassiset ongelmat

Matematiikassa klassisiksi ongelmiksi kutsutaan kolmea geometrista konstruktio-ongelmaa: kuution kahdentamista, kulman jakoa kolmeen osaan ja ympyrän neliöintiä. Suhteessa ongelmien ikään onkin yllättävää, että niiden mahdottomaksi todistamiseen tarvitaan niinkin uutta matematiikan haaraa kuin abstraktia algebraa.

Viimenumeron pääkirjoituksessa mainitun legendan mukaan jumalat vaativat, että kuution muotoisen alttarin tilavuus pitäisi kahdentaa. Piti siis muodostaa vanhan alttarin sivua käyttäen uuden, tilavuudeltaan kaksinkertaisen alttarin sivu. Tähän kreikkalaiset eivät kuitenkaan harpilla ja viivaimella tietenkään pystyneet. Olkoon alkuperäisen alttarin sivun pituus yksikköjana. Tällöin yritetään piirtää luku, joka toteuttaisi yhtälön x³-2=0. Tällä yhtälöllä ei ole rationaalijuuria, sillä mikään mahdollisista vaihtoehdoista (-2, -1, 1, 2) ei toteuta yhtälöä. Sen juuri ei siis ole piirrettävä luku.

Kulman jako kahteen osaan on helppoa, mutta kulman jakaminen kolmeen osaan on tietyissä tapauksissa mahdotonta. Piirretään annettu kulma 3a yksikköympyrään käsittelyn helpottamiseksi. Kun tiedetään kulma 3a, tiedetään myös cos 3a. Kulma a on piirrettävissä täsmälleen silloin, kun cos a on piirrettävissä. Nyt saadaan kolmannen asteen yhtälö:

cos 3a = 4 cos³ a - 3 cos a

4 x³-3x-t=0

(x = cos a, t = cos 3a)

Jos valitaan 3a=90°, saadaan yhtälö 4 x³-3x=0, jolle löytyy piirrettävä ratkaisu /2. Suora kulma voidaan siis jakaa kolmeen osaan. Sen sijaan valinta 3a=60° antaa yhtälön 8 x³-6x-1=0, jolla ei ole rationaalisia juuria. 60° kulmaa ei siis voida jakaa kolmeen yhtä suureen osaan. Tämä vastaesimerkki riittää osoittamaan, että yleistä tapaa jakaa kulma kolmeen yhtä suureen osaan ei ole.

Suorakulmion neliöinti tarkoittaa sitä toimenpidettä, kun muodostetaan neliö, jonka pinta-ala on sama kuin annetun suorakulmion. Tämä voidaan suorittaa melko helposti, koska tällaisen neliön pinta-alahan on sivujen tulojen neliöjuuri. Ympyrän neliöinnissä on vastaavasti muodostettava neliö, jonka pinta-ala on sama kuin annetun ympyrän. Jos annetun ympyrän sädettä käytetään yksikköjanana, on ympyrän pinta-ala p, jolloin neliön sivun pituus on . Jos luku on piirrettävä, myös luku p on piirrettävä. Tällöin kunta, joka sisältää luvun p on n asteen kuntalaajennus. Tällöin kuitenkin olisi olemassa rationaalikertoiminen n asteen polynomi, jonka nollakohta p olisi. Tämä on ristiriita, sillä p on transsendenttinen luku, mikä tarkoittaa sitä, että ei ole olemassa mitään rationaalilukukertoimista polynomia, jonka nollakohta p olisi. Tämä voidaan ilmaista, myös siten, että transsendenttisen luvun sisältävän kunnan laajennuksen aste on ¥, joka ei ole kakkosen potenssi.

Piirrettävät monikulmiot

Samalla tavalla kuin kulman jaossa kolmeen osaan, säännöllisten monikulmioiden piirtäminen on mahdollista tietyissä erikoistapauksissa, mutta yleisessä tapauksessa se ei onnistu. Tässä tapauksessa käsittelyyn tarvitaan lisäksi Galois'n-teoriaa2), joka tunnetaan parhaiten siitä, että sillä voidaan osoittaa se, että yli neljännen asteen yhtälöille ei ole yleistä ratkaisukaavaa juurten avulla. Monikulmion konstruoimiseen vaaditaan hieman samaan tapaan kuin kulman jaossa kolmeen osaan luvun konstruointia, ja Galois'n-teorian avulla voidaan osoittaa, että pienimmän kunnan, joka sisältää laajennuksen aste on , jossa f(n) on Eulerin f-funktio. f(n) merkitsee niiden lukujen määrää, jotka ovat pienempiä kuin n, ja niillä ei ole yhteisiä tekijöitä n kanssa. Otetaan esimerkiksi f(15). Luvuilla 1, 2, 4, 7, 8, 11, 13 ja 14 ei ole yhteisiä tekijöitä 15 kanssa, siispä f(15) = 8. Kuten aikaisemminkin, laajennuksen asteen on oltava kakkosen potenssi. Tässä tapauksessa siis säännöllinen n-kulmio (n ³ 3) on piirrettävä, mikäli on kakkosen potenssi. Tämän voi ilmaista myös toisella tavalla siten, että n-kulmio on piirrettävä, jos sen kakkosesta poikkeavat tekijät ovat Fermat’n alkulukuja (kuitenkin eri alkulukuja). Fermat’n alkuluvuksi kutsutaan alkulukua muotoa . Näin ensimmäiset ei-piirrettävät monikulmiot ovat 7-, 9-, 11-, 13- ja 14-kulmiot. Kun n kasvaa, piirrettävien n-kulmioiden osuus pienenee. Piirrettäviä monikulmioita on kuitenkin hyvin isoilla n arvoilla, kuten esimerkiksi 65537-kulmio (65537 on Fermat’n alkuluku). Tällainen puhtaan algebrallinen lähestymistapa ei kuitenkaan kerro itse konstruoinnin tapahtumisesta mitään. Tällaisessa tapauksessa tieto, että 65537-kulmio voidaan konstruoida on varmasti hyödyllisempi kuin tarkka selitys siitä miten se tapahtuisi.

Veli Peltola

Kirjallisuutta

[1] Pogorelov, A.; Geometry. Mir Publishers 1987

[2] Hanneken, C. B.; Introduction to Abstract Algebra. Dickenson Publishing Company, Inc., Belmont, California 1968