[an error occurred while processing this directive]
Juurta jaksain
Joskus peruskouluaikanani opin, että yhtälön x2=2 ratkaisu
oli irrationaalinen, toisin sanoen että sen tarkka arvo ilmaistiin
merkinnällä 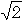 . Kerrassaan kiehtova luku: ei kokonaisia, jakoviivoja
eikä osia. Luontoa murto- ja luonnollisin luvuin kuvanneita Pythagoraan
oppilaita tyydyttävästä ratkaisusta tämän erottaa vain kaunis pikku
ärrästä muovailtu merkki. Sittemmin lukiossa sain yksinkertaisuudessaan
kodikkaan todistuksen sille havainnoimalleni tosiasialle, että
luonnollisten lukujen neliöjuuret tosiaan olivat vain joko toisia
luonnollisia lukuja tai irrationaalilukuja. Sääliksi kävi pythagoralaisia.
. Kerrassaan kiehtova luku: ei kokonaisia, jakoviivoja
eikä osia. Luontoa murto- ja luonnollisin luvuin kuvanneita Pythagoraan
oppilaita tyydyttävästä ratkaisusta tämän erottaa vain kaunis pikku
ärrästä muovailtu merkki. Sittemmin lukiossa sain yksinkertaisuudessaan
kodikkaan todistuksen sille havainnoimalleni tosiasialle, että
luonnollisten lukujen neliöjuuret tosiaan olivat vain joko toisia
luonnollisia lukuja tai irrationaalilukuja. Sääliksi kävi pythagoralaisia.
Juuriin liittyy roppakaupalla muitakin viehättäviä ominaisuuksia.
Yritetäänpä esimerkiksi sittenkin vääntää kahden neliöjuurta murtoluvuksi.
Jos aloitamme approksimaatiosta 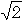 »1/1, löytyvät parhaat likiarvot jako-osien
määrän kasvaessa kohdista 1/1, 3/2, 7/5, 17/12, 41/29, 99/70, 239/169, 577/408...
edellisestä likiarvosta muotoa a/b saadaan siis seuraava laskemalla (a+2b)/(a+b).
Tämä algoritmi tunnettiin jo toisella vuosisadalla.
»1/1, löytyvät parhaat likiarvot jako-osien
määrän kasvaessa kohdista 1/1, 3/2, 7/5, 17/12, 41/29, 99/70, 239/169, 577/408...
edellisestä likiarvosta muotoa a/b saadaan siis seuraava laskemalla (a+2b)/(a+b).
Tämä algoritmi tunnettiin jo toisella vuosisadalla.
Likiarvosarjan jäsenet ovat itsekin vähän erikoisia. Otetaanpa esimerkiksi
mikä tahansa sarjan murtoluku a/b, jossa sekä nimittäjä että osoittaja ovat
parittomia (joka toinen sarjan jäsen toteuttaa tämän ehdon). Valitaan luvut
c ja d siten, että c+d=a ja c=d+1. Tällöin luvut c, d ja b kuvaavat
suorakulmaista kolmiota toteuttaen Pythagoraan teoreeman: c2+d2=b2.
Kaunis 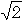 :n ominaisuus liittyy sen monikertoihin: luetellaan ne peräkkäin
jättäen desimaaliosat pois: 1 2 4 5 7 8... Jos väliin jäävät luvut
järjestetään toiseksi jonoksi (3 6 10 13 17 20...), on jonojen n:nsien
jäsenten erotus 2n.
:n ominaisuus liittyy sen monikertoihin: luetellaan ne peräkkäin
jättäen desimaaliosat pois: 1 2 4 5 7 8... Jos väliin jäävät luvut
järjestetään toiseksi jonoksi (3 6 10 13 17 20...), on jonojen n:nsien
jäsenten erotus 2n.
Legenda muinaisesta Ateenasta opettaa, ettei juurten kanssa kannata möhliä.
Ateenalaiset kysyivät oraakkelilta, kuinka ennalta torjua ruton kirous. Neuvoksi
he saivat kaksinkertaistaa kuutionmuotoisen Apollon alttarin koon.
Ateenalaisraukat eivät älynneet, että ratkaisu piilee kuutiojuuren
laskemisessa, vaan rakensivatkin kahdeksankertaisen alttarin
kaksinkertaistamalla sen sivun. Musta surma iski.
Geometriasta kiinnostuneet voivat muuten halutessaan lähettää Seepialle
ehdotuksia 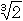 :n esittämisestä geometrisesti. Lähimmäs osunut esitys saa
tunnustuspalkinnon, mikäli piirros on selkeä tai edes lukukelpoinen.
:n esittämisestä geometrisesti. Lähimmäs osunut esitys saa
tunnustuspalkinnon, mikäli piirros on selkeä tai edes lukukelpoinen.
Jaakko Kortesharju
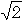 . Kerrassaan kiehtova luku: ei kokonaisia, jakoviivoja
eikä osia. Luontoa murto- ja luonnollisin luvuin kuvanneita Pythagoraan
oppilaita tyydyttävästä ratkaisusta tämän erottaa vain kaunis pikku
ärrästä muovailtu merkki. Sittemmin lukiossa sain yksinkertaisuudessaan
kodikkaan todistuksen sille havainnoimalleni tosiasialle, että
luonnollisten lukujen neliöjuuret tosiaan olivat vain joko toisia
luonnollisia lukuja tai irrationaalilukuja. Sääliksi kävi pythagoralaisia.
. Kerrassaan kiehtova luku: ei kokonaisia, jakoviivoja
eikä osia. Luontoa murto- ja luonnollisin luvuin kuvanneita Pythagoraan
oppilaita tyydyttävästä ratkaisusta tämän erottaa vain kaunis pikku
ärrästä muovailtu merkki. Sittemmin lukiossa sain yksinkertaisuudessaan
kodikkaan todistuksen sille havainnoimalleni tosiasialle, että
luonnollisten lukujen neliöjuuret tosiaan olivat vain joko toisia
luonnollisia lukuja tai irrationaalilukuja. Sääliksi kävi pythagoralaisia.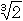 :n esittämisestä geometrisesti. Lähimmäs osunut esitys saa
tunnustuspalkinnon, mikäli piirros on selkeä tai edes lukukelpoinen.
:n esittämisestä geometrisesti. Lähimmäs osunut esitys saa
tunnustuspalkinnon, mikäli piirros on selkeä tai edes lukukelpoinen.