Kultaien leikkaus ja Fibonaccin luvut esiintyvät luonnossa lähes kaikkialla. Joskus niiden merkitys on selvä, kuten esimerkiksi kuvattaessa eläinpopulaation kokoa, mutta kun ne löytyvät kasvin siementen lukumääristä tai niiden osien kokosuhteista, yhteys näyttää lähinnä sattumalta. Kasveilla on kuitenkin hyvät evolutiiviset perusteet noudattaa näitä lukuja. Erityisesti ne ilmenevät samankaltaisten kasvin osien keskinäisessä sijoittumisessa eli fyllotaksiassa. Kasvien lisäksi samaa teoriaa voidaan soveltaa esimerkiksi simpukankuorten täpliin tai muurahaiskävyn suomuihin.
Esimerkiksi auringonkukan tai päivänkakkaran mykerössä siemenet näyttävät sijoittuvan spiraaleihin, joista toinen kiertää myötäpäivään ja toinen vastapäivään. Näiden spiraalien lukumäärät ovat lähes poikkeuksetta peräkkäisiä Fibonaccin lukuja. Luvut vaihtelevat kukinnon koon mukaan: Keskikokoisissa auringonkukan mykeröissä on yleensä nähtävissä 34 toiseen suuntaan ja 55 toiseen suuntaan kaartuvaa spiraalia. Suuremmissa nämä luvut saattavat olla 55 ja 89, tai jopa 89 ja 144. Pienemmissä puolestaan 21 ja 34 tai 13 ja 21. Yleisesti, jos mykerössä näkyy m spiraalia myötäpäivään ja n vastapäivään, sillä sanotaan olevan (m, n) fyllotaksia.
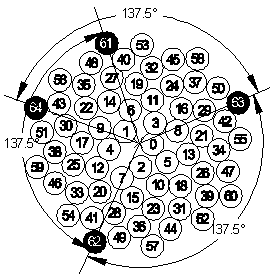
Auringonkukan mykeröiden on havaittu noudattavan yksinkertaista mallia, jonka mukaan jokainen kukka sijaitsee aina samassa kulmassa (d) edelliseen nähden. Tätä kulmaa kutsumme poikkeamakulmaksi. Tällöin N:nen kukan paikka voidaan ilmaista napakoordinaatistosa seuraavasti:
|
|
(1) |
missäf on sen positiivisen x-akselin kanssa muodostama kulma ja r sen etäisyys origosta. c on kukkien koosta riippuva vakio, joka määrää etääntymisnopeuden keskipisteestä. (Kuva 1)
Kaikki kukat sijaitsevat spiraalilla, jonka lauseke saadaan
yhtälöstä (1), kun N:lle annetaan kaikki
positiiviset Reaalilukuarvot. Tätä spiraalia kutsumme
tuotantospiraaliksi. Yhtälön (1) esittämän
spiraalin valinta on perusteltua. Tällöin kukat
sijoittuvat yhtä tiheästi kaikilla
etäisyyksillä keskustasta, koska minkä tahansa
säteen sisään jäävien kukkien
määrä on tällöin verrannollinen
vastaavan ympyrän pinta-alaan, joka puolestaan on
verrannollinen säteen neliöön. Tällaista
spiraalia kutsutaan syklotronispiraaliksi1).
Tuotantospiraalille voidaan käyttää muitakin
lausekkeita. Esimerkiksi Arkimedeen spiraali, jossa antaa paremman kuvan kehittyvästä
mykeröstä, jossa reunakukat ovat pidemmälle
kehittyneitä kuin kukat keskustassa.
Lähes kaikissa kasveissa havaitaan poikkeamakulma:
|
|
(2) |
,
|
Kuva 1: Kaavakuva mykerön keskustasta |
missä , eli kultaisen
leikkauksen suhde! Auringonkukassa näyttäisi siis
esiintyvän sekä kultainen leikkaus että Fibonaccin
luvut ilman mitään selvää syytä.
Sama ilmiö esiintyy lehtien asettumisessa varren ympäri. Lehdet näyttävät kiertävän varren ympäri siten, että päällekkäin osuvien lehtien väli olisi aina jonkin Fibonaccin luvun ilmoittama määrä lehtiä. (Itse asiassa lehdet eivät koskaan asetu täysin päällekkäin, sillä d on irrationaalinen.)
On monia syitä siihen miksi evoluutio on suosinut näitä lukuja. Mykerössä on edullisinta olla mahdollisimman monta siementä pinta-alayksikköä kohti, ja lehtien tulisi sijaita mahdollisimman kaukana toisistaan, jotta ne kaikki saisivat riittävästi valoa eivätkä varjostaisi toisiaan. Voidaan osoittaa, että Fibonaccin lukuja ja kultaista leikkausta noudattamalla kasvit saavuttavat itselleen edullisimman rakenteen.
Saattaa vaikuttaa oudolta, että mykerön koon kasvaessa spiraalien määrä muuttuu hyppäyksittäin, vaikka kasvu olisikin tasaista. Itse asiassa spiraalit eivät lainkaan synny ja katoa, vaan kaikki spiraalisarjat ovat olemassa koko ajan. Mykeröstä hahmottuvat kuitenkin parhaiten ne spiraalit, joihin kuuluvat kukat koskettavat toisiaan. Tällaisten spiraalien sanotaan olevan yhtenäisiä. Samaan spiraaliin kuuluvien peräkkäisen kukkien järjestysnumeroiden erotus on aina vakio. Spiraalia, jolle tämä erotus on m sanotaan m-spiraaliksi. Kukinnon kaikki m-spiraalit muodostavat m-spiraalisarjan, jossa on m rinnakkaista spiraalia. Kaikkien tietyn spiraalin kukkien järjestysluvut kuuluvat siis samaan jäännösluokkaan (mod m).
Saman spiraalin kukkien välimatkaan vaikuttaa säteen r muutos toisesta toiseen siirryttäessä. Koska r ilmaistaan neliöjuurifunktiolla, tämä on luonnollisesti sitä pienempi, mitä kauempana keskustasta kukat sijaitsevat. Etäisyyteen vaikuttaa toisaalta myös kukkien välinen kulma. Tietyssä kulmassa toisiinsa nähden sijaitsevat kukat ovat sitä kauempana toisistaan, mitä kauempana ympyrän keskustasta ne sijaitsevat. Näin voidaan todeta, että jokin spiraalisarja on näkyvissä vain tietyllä etäisyysvälillä keskustasta. Itse asiassa etäisyys keskustasta on ainoa spiraalien näkyvyyteen vaikuttava tekijä. Esimerkiksi kukkien koolla tai määrällä ei ole merkitystä.
Kukinnon kasvaessa reuna-alueelle syntyvän uuden spiraalisarjan spiraalien määrä on aina kahden edellisen spiraalisarjan summa. Tämä spiraaleille ominainen ilmiö tunnetaan summautumisena.
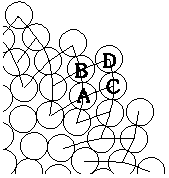
|
Kuva 5: |
Oletetaan että jollakin tietyllä etäisyysalueella mykerön keskustasta on havaittavissa m myötäpäivään ja n vastapäivään kiertävää spiraalia. Näihin sarjoihin kuuluu silloin m ja n spiraalia vastaavasti. Kuvassa 5 kukat A ja D ovat yhteydessä toisiinsa ainoastaan kukkien B ja C välityksellä. Kukasta A kukkaan B siirryttäessä on järjestysnumeroon lisättävä n, ja vastaavasti B:stä D:hen siirryttäessä on lukuun lisättävä m. Tällöin A:sta D:hen siirryttäessä on lisättävä vastaavasti n+m.
Mykerön kasvaessa kukat siirtyvät pitkittäissuunnassa lähemmäs toisiaan, jolloin A ja D kohtaavat ja uusi spiraalisarja tulee näkyviin. Tämän spiraalisarjan peräkkäisten kukkien järjestysnumeroiden erotus on m+n. Sillä etäisyydellä keskustasta, jolla m+n sarjan kukat ensimmäisen kerran koskettavat toisiaan, on havaittavissa kolme yhtenäistä spiraalisarjaa. Kauemmaksi siirryttäessä n- ja m-sarjoista pienempi lakkaa olemasta yhtenäinen ja häviää näkyvistä. Spiraalien lukumäärät eri alueilla keskustasta alkaen muodostavat siis lukujonon, jonka jokainen luku on kahden edellisen summa. Tällaisista sarjoista yksinkertaisin on Fibonaccin jono (1, 1, 2, 3, 5, 8, 13, 21, 34, ...), joka, kuten aiemmin todettiin, esiintyy yli 92%:ssa kasveista. Toiseksi yleisin on noin 2%:ssa tapauksista esiintyvä ns. Lucas-jono (1, 3, 4, 7, 11, 18, 29, 47, 76, ...), joka muodostetaan kuten Fibonaccin jono, mutta lähtien luvuista 1 ja 3.
Hieman toisenlainen yfllotaksia esiintyy esimerkiksi ananaksessa tai suovehkassa. Tässä mallissa kukkien voidaan ajatella sijoittuvan sylinterin pinnalle. Ne ovat siis aina yhtä kaukana sylinterin akselista. Kukkien paikka voidaan ilmaista seuraavasti:
|
|
(4) |
missä f, r ja H ovat kukan
sylinterikoordinaatit. Laskutoimitusten helpottamiseksi
käytämme kulmayksikkönä radiaaneja (). Tällöin kulman lukuarvo on yhtä suuri kuin
ympyrän kaarta pitkin kuljettu etäisyys sylinterin
pinnalla.
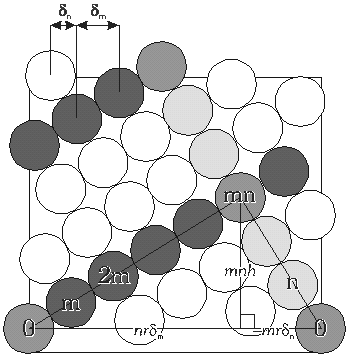
|
Kuva 6: Auki leikattu sylinteri, jolla sijaitsevat sylinterit ilmentävät (m,n)-fyllotaksiaa. Sylinteri saadaan, kun kuvan suorakaiteen oikea ja vasen reuna liimataan yhteen. |
Koska sylinterimallissa säde on vakio, ei poikkeamakulmaa (d) tarvitse valita siten, että pakkaustehokkuus olisi optimaalinen millä tahansa säteellä. Itse asiassa dvoi olla mikä tahansa reaaliluku tietyltä väliltä. Yleensä se on kuitenkin lähellä Fibonaccin kulmaa, sillä silloin fyllotaksia säilyttää tehokkuutensa, vaikka kukinnon muoto ja koko muuttuisivat kasvin kasvaessa, ja sylinteri voi myös olla eri kohdista eri paksuinen. Tästä seuraa, että myös sylinterifyllotaksiassa näkyvät spiraalisarjat ilmentävät yleensä Fibonaccin lukuja.
d:n valinnan jälkeen tehtäväksi jää vielä määrittää kaavan (4) muut vakiot sen mukaisiksi.
Kuva 6 esittää (3, 5) fyllotaksiaa ilmentävää auki leikattua sylinteriä. Eri vakioiden keskinäisten suhteiden määrittämisessä voidaan hyödyntää kahden kukasta 0 lähtevän spiraalin leikkauspisteiden välille piirrettyä kolmiota ja kosinilausetta. Ne lukijat, jotka eivät halua seurata näitä matemaattisia perusteluja voivat hypätä suoraan alaotsikkoon ”Pakkaustehokkuus”.
Merkitään kuvassa esiintyvistä spiraalisarjoista oikealle kiertävää m:llä ja vasemmalle kiertävää n:llä.
Kiertokulma kukasta 0 kukkaan m on
määritelmän (4) mukaan . Tämä kulma voidaan ilmaista kahdessa osassa:
[14]
|
|
(5) |

|
Kuva 7: Komealupiini (Lupinus poluphyllus) on typillinen esimerkki sylinterifyllotaksiasta. |
missä Dm on
dm täyskierroksina
ilmaistuna ja pyöristettynä lähimpään
kokonaislukuun, ja on 0:n ja m:n
välinen ”todellinen kulma”, eli itseisarvoltaan
pienin 0:n ja m:n välinen kulma2).
(Kukkien sijainti ilmaistaan sylinterikoordinaatistossa, joten
kulmat ovat aina vaakasuuntaisia mittayksiköitä ja
pituusmitat pystysuuntaisia.) Nämä yhtälöt
voidaan kirjoittaa vastaavasti toiselle spiraalisarjalle, kun
m:t korvataan n:illä. Koska kukka m
sijaitsee kukan 0 oikealla ja n vasemmalla puolella, dm on luonnollisesti positiivinen
ja dn negatiivinen,
sillä kukka n sijoittuu aina kukan 0 vasemmalle ja
m oikealle puolelle. Koska 0-kukasta lähtevät
m- ja n-spiraalit kohtaavat kukassa mn,
saadaan:
|
|
(6) |
(yhtälö on kirjoitettu vähennyslaskuna,
sillä ) Sijoittamalla dm
ja dn
yhtälöstä (5), saadaan vastaavasti:
|
|
(7) |
Saamme lisää selville spiraalien geometriasta, kun sovellamme Pythagoraan lausetta kuvan 6 kahteen suorakulmaiseen kolmioon. Näin saadaan:
|
|
(8) |
|
|
(9) |
missä d on kukkien halkaisija, joka on yhtä suuri kuin saman spiraalin peräkkäisten kukkien välinen etäisyys kun kukat koskettavat toisiaan. Yhtälöt voidaan ratkaista d:n ja h:n suhteen:
|
|
(10) |
|
|
(11) |
Binomikaavaa käyttämällä (11) voidaan muuttaa muotoon:
d=
|
= |
(12) |
Yhtenäisten spiraalien välinen kulma saadaan kun
merkitään m- ja n-spiraalisarjojen
välistä kulmaa g:lla, ja kun tiedetään, että kolmion
kanta on , voidaan kosinilauseen mukaan kirjoittaa
seuraavasti:
|
|
(13) |
Kolmas hyödyllinen kaava on ns. Heronin kaava, joka ilmaisee kolmion pinta-alan sen sivujen pituuksien avulla:
|
|
(14) |
missä a, b ja c ovat kolmion sivut
ja , eli kolmion piirin puolikas. Kun
tiedetään, että kolmion ala on
, voidaan yhtälöstä (14) ratkaista
h:
|
|
(15) |
Tästä voidaan ratkaista kuvan 6 kolmion korkeus, sillä
a=2pr, b=nd, c=md
ja
.
Esimerkki:
Eräässä 2cm paksussa kuusenkävyssä havaittiin suomujen muodostavan 8 spiraalia toiseen suuntaan ja 5 toiseen. Kahden peräkkäisen suomun välimatka on noin 6,2mm. Määritä kahden peräkkäisen suomun välinen poikkeamakulma (d) sekä pystypoikkeama (h).
Ratkaisu:
Tässä tapauksessa m=8 ja n=5. Yhtälöstä (15) saadaan:
|
|
(16) |
jossa
| p
|
sijoittamalla nyt p kaavaan (16) saadaan:
h
d:n ratkaiseminen ei ole yhtä yksinkertaista. Se saadaan yhtälöstä (5), mutta ensin on ratkaistava Diofantoksen yhtälö3) (7) sekä dm tai dn yhtälöistä (8) tai (9).
Emme tarvitse yhtälön (7) kaikkia ratkaisuja; – ainoastaan pienimmät positiiviset ratkaisut. Ne on helppo arvata, mutta ne voidaan ratkaista myös Eukleideen algoritmilla. Näin saadaan:
.
Yhtälöstä (8):
Kun Dm ja dm sijoitetaan yhtälöön (5) saadaan:
Vastaus:
Kuten havaittiin muiden vakioiden selvittäminen on melko yksinkertaista kun tunnetaan d, h tai d, sekä yhtenäiset spiraalisarjat. Näitä arvoja ei kuitenkaan voida valita miten tahansa. Tietty spiraalisarja voi nimittäin olla yhtenäinen vain tietyillä d:n, h:n ja d:n arvoilla. Esimerkiksi h:n kasvessa tarpeeksi suurempi yhtenäisistä spiraalisarjoista menettää yhtenäisyytensä, sillä sen ja toisen yhtenäisen spiraalisarjan välinen kulma laskee alle 60°:n, jolloin kukat eivät yksinkertaisesti enää mahdu vierekkäin. (h:n kasvaminen vastaa tavallaan kuvion venymistä pystysuunnassa, paitsi että d kasvaa vastaavasti säilyttäen vierekkäisten kukkien kosketuksen mikäli mahdollista.) Vastaavasti h:n pienentyessä pienin spiraalisarja menettää yhtenäisyytensä kun g ylittää 120°. h:lle ja d:lle voidaan siis määrittää arvoalueet, joilla tietty spiraalisarja voi olla yhtenäinen. Valittaessa arvot näiden alueiden reunalta, saadaan kukat sijoittumaan siten, että kolme spiraalisarjaa ovat yhtenäisiä. Tällöin niiden kaikkien väliset kulmat ovat 60°.
Nämä raja-arvot saadaan yhtälön (13)
avulla, kun sijoitetaan . Kun
tiedetään, että
, saadaan:
.
ja kun korvataan d yhtälöllä (12) voidaan kirjoittaa:
,
mistä voidaan yhtälön (6) avulla ratkaista dm ja dn:
|
|
(17) |
Kun dm:lle ja dn:lle
annetaan nämä arvot, ja määritetään
muut arvot kuten edellä, saadaan fyllotaksiakuvio, jossa on
3 yhtenäistä spiraalisarjaa: m, n ja . Toinen raja, jolla yhtenäiset spiraalisarjat
ovat m, n ja m+n saadaan vastaavasti kun
. Tällöin 60°kulma esiintyy samoin kuin edellisessä
tapauksessa, mutta ei m:n ja n:n vaan
:n ja m+n :n välillä. Koska
saadaan vastaavasti:
ja
|
|
(18) |
Nyt voidaan todeta, että spiraalisarjat m ja n voivat olla yhtenäisiä jos ja vain jos dm ja dn sijaitsevat lausekkeiden (17) ja (18) määräämällä suljetulla välillä.
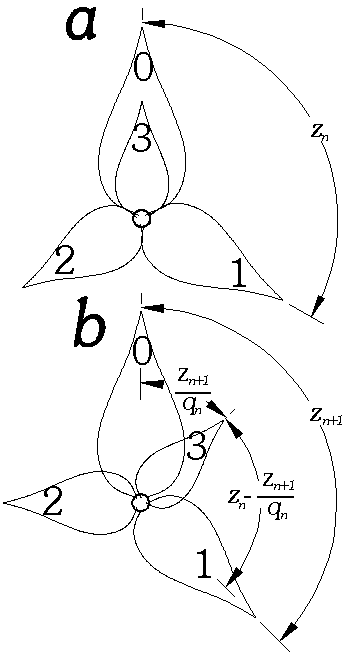
|
Kuva 8: Siirtyminen z:n approksimaatiosta zn arvoon zn+1. Kuvat on piirretty siten, että n=0 ja zn=z0=1/3. Kuvasta b näkyy, kuinka lehti 3 jakaa lehtien 0 ja 1 välin suhteessa zn+1:(1-zn+1). |
Poikkeamakulman t valintaa voi perustella monella tavalla.
Kasville olisi edullisinta, että kukat tai lehdet jakautuisivat mahdollisimman tasaisesti eri kulma-alueiden kesken kukkien määrästä tai mittakaavasta riippumatta. Tämän perusteella voidaan olettaa, että varteen syntyvä uusi lehti syntyy aina suurimpaan olemassa olevaan rakoon kahden muun lehden välillä (a). Tasaisesta jakaumasta seuraa myös, että kukat sijaitsevat pienessä mittakaavassa samoin kuin suuressakin mittakaavassa. Näin on, jos uusi lehti jakaa sen välin, johon se syntyy samassa suhteessa, kuin d jakaa täyskulman (b).
Näiden oletusten pohjalta voidaan johtaa kulman d optimaalisin arvo seuraavasti: [16]
Tarkastellaan varren ympärille asettuvien lehtien
muodostamaa kuviota ylhäältä päin. (Kuva
8a) Merkitään z:lla kahden lehden
välistä kulmaa kierroksina ilmaistuna. Toisin sanoen
. z:n on luonnollisesti oltava irrationaaliluku,
sillä muutoin f:lla voisi olla vain äärellinen
määrä arvoja, mikä johtaisi kukkien
epätasaiseen jakautumiseen (kuva 1). Sitä voidaan
kuitenkin lähestyä rationaalisilla likiarvoilla siten,
että uusi arvo on aina lähempänä z:n
todellista arvoa kuin edellinen. Olkoon
luvun z n:s likiarvo, jossa
pn ja qn ovat
suhteellisia alkulukuja ts. niillä ei ole yhteisiä
tekijöitä. Arvataan jokin likiarvo z:lle ja
merkitään sitä z0:lla. Esim.
ts. pn=1 ja
qn=3. Lehdet osuvat kohdakkain aina
qn lehden välein, jolloin on
käännytty yhteensä pn
täyskierrosta (koska
, joka on kokonaisluku).
qn:s lehti osuu siis kohdakkain 0:nnen
lehden kanssa jne.
Lehtien kohdakkain sattumisen välttämiseksi
kasvatetaan likiarvoa hieman. Merkitään tätä
uutta likiarvoa zn+1:llä.
qn:s lehti sijoittuu tällöin
ylhäältä katsottuna lehden 0 ja sitä
lähinnä olevan lehden väliin jakaen sen oletuksen
b mukaisesti suhteessa zn+1 :
1– zn+1. (huomaa, että
ylhäältä katsottuna 0:aa lähin lehti ei
välttämättä lehti 1) Tämän
välin suuruus on aina (=zn, kun
pn=1 eli kun lehti numero 0 on lähinnä
lehteä numero 1). Tällöin
qn:nen lehden kierokulma ei
enää olekaan pn×360°vaan
=
(qn:nen lehden paikka
ympyrän kehällä saadaan kun
käännytään qn kertaa
)
Ratkaistaan z
|
Û Û Û |
|
= = = = |
Toisaalta kuitenkin , joten
|
|
(3) |
Kun valitaan
, niin (3) on tosi jos ja vain jos
pn ja qn ovat
peräkkäisiä parillista järjestyslukua olevia
Fibonaccin lukuja. Tämä ominaisuus voidaan johtaa
Fibonaccin lukujen perusominaisuudesta 1 (kss. 30).
z:n arvo saadaan, kun tiedetään, että peräkkäisten Fibonaccin lukujen suhde lähenee kultaista leikkausta, kun luvut lähenevät ääretöntä.
Kolmas tapa lähestyä d:n optimaalisinta arvoa on pakkaustehokkuus. Tällöin ajatellaan, että kasville olisi edullisinta saada mahdollisimman monta kukkaa mahtumaan tietyn kokoiseen mykeröön.
Pakkaustehokkuudella tarkoitetaan yleisesti hyödynnetyn alan suhdetta koko alaan, eli mykerossä kukkien yhteenlasketun pinta-alan suhdetta koko mykerön alaan. Keskenään saman kokoisten ympyrän muotoisten kukkien fyllotaksiaa tutkittaessa voidaan kuitenkin käyttää toista määritelmää, joka johtaa samoihin lukuarvoihin, mutta tekee laskut helpommiksi. [15]
Kaavan (1) mukaan kukkien etäisyys keskipisteestä
noudattaa kaavaa , sillä
tällöin mykeröön mahtuvien kukkien
määrä on suoraan verrannollinen mykerön
pinta-alaan. Kukat ovat siis laajassa mittakaavassa sijoittuneet
tasaisesti. Yleisesti voidaan sanoa, että miten tahansa
äärettömälle tasolle sijoittuneet pisteet
sijaitsevat laajassa mittakaavassa tasaisesti, jos jossakin
kohtaa tasolla sijaitsevan ympyrän sisään
jäävien pisteiden lukumäärän suhde
ympyrän säteeseen lähenee jotakin vakiota kun
ympyrän säde lähestyy
ääretöntä. Toisin sanoen on olemassa
raja-arvo:
|
|
(19) |
jossa Nr on r-säteisen
ympyrän sisään jäävien kukkien
lukumäärä. Esimerkiksi spiraaliyfllotaksialla
A on tällöin . Lauseke (19)
voidaan tulkita siten, että A on
keskimääräinen pinta-ala kukkaa kohden.
Pienessä mittakaavassa tilanne on kuitenkin toinen. Kukat saattavat sijoittua kaikki samalle suoralle tai suuriin kaukana toisistaan oleviin ryppäisiin ja olla silti suuressa mittakaavassa tasaisesti sijoittuneita. Tällainen pakkaaminen ei kuitenkaan ole erityisen tehokasta, sillä jos kaikki kukat ovat yhtä suuria, määrää pienin kahden kukan väli suurimman mahdollisimman koon. Itse asiassa riittää, että tarkastelemme pienintä kahden kukan välistä etäisyyttä, sillä jos jossakin on kukkia keskimääräistä tiheämpään pakattuna, niitä täytyy jossakin muualla olla keskimääräistä harvemmassa.
Määrittelemme nyt pakkaustehokkuuden seuraavasti:
|
|
(20) |
missä D on pienin etäisyys joka voidaan mitata kahden kukan keskipisteiden välillä. A:n pinta-alatulkinnan perusteella (20) on yhtäpitävä pakkaustehokkuuden pinta-alamääritelmän kanssa.
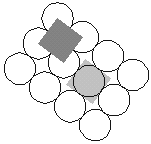
|
Kuva 9: |
Sylinterifyllotaksian pakkaustehokkuuden
määrittäminen on varsin yksinkertaista, sillä
keskimääräinen pinta-ala kukkaa kohden on
neljän kukan muodostaman suunnikkaan ala. (ks. kuva 9) ts.
, missä
on yhtenäisten
spiraalisarjojen välinen kulma.
Pienin etäisyys kahden kukan välillä on
d, kun , mutta pienemmillä
kulmilla kukat menevät osittain päällekkäin
ja välimatkaksi saadaan
.
Tällöin
|
|
(21) |
sillä .
h saavuttaa tällöin
maksimiarvonsa kun :
Spiraalifyllotaksialle h:ta on
vaikea määrittää, mutta lähteessä
[15] osoitetaan, että se saa maksimiarvonsa »0,8169, kun d=t–2. Spiraalifyyllotaksian
pakkaustehokkuus jää siis parhaimmillaankin
selvästi sylinterisestä jälkeen. On kuitenkin
helppoa osoittaa, että jos d on rationaaliluku, niin h=0. [15]

|
Kuva 4: Kukkien sijoittuminen mykerössä liittyy pakkaamisongelmaan. Tehokkaassa pakkaamisessa tila jakaantuu mahdollisimman tasaisesti kukkien kesken. Kaikkein suurin pakkaustehokkuus (h»0,8169) saavutetaan poikkeamakulmalla d=t×360°»137,5077 (a). Kukat mahtuvat huonommin, kun käytetään t:n rationaalista approksimaatiotad=21/55×360°»137,454545... (b) tai irrationaalista approksimaatiota d=t(155+Ö13)/414×360°»137,9179... (b) |
Vaikuttaa siis siltä, että Fibonaccin lukuja ja kultaista leikkausta ”hyödyntämällä” kasvit voivat sijoittaa osasensa mahdollisimman tehokkaasti, mutta miten kasvit osaavat noudattaa näitä sääntöjä? Millä tavalla kasvi määrää, että kahden peräkkäin syntyneen kukan välinen kulma on juuri 137,5°, varsinkin kun mykerön kukat eivät näytä edes syntyvän yksitellen? Mistä kukka syntyessään tietää, mihin kohtaan on hetkeä aikaisemmin syntynyt kukka mykerön vastakkaisella laidalla? Näihin kysymyksiin on kehitetty vastaukseksi useita teorioita, joista mitään ei ole voitu täysin kumota. Vaikuttaakin itse asiassa siltä, että eri kasvit käyttävät eri menetelmiä saman tuloksen saavuttamiseksi.
Jo pitkään on tiedetty, että kasvien kasvuun vaikuttavat erilaiset aktivaattoreina ja inhibiittoreina toimivat hormonit5). Jokaisen oksan kärkiosassa syntyy inhibiittorihormonia, joka estää ylimääräisten haarojen syntymistä sen lähettyville. Levitessään hormoni laimenee, ja sen vaikutus heikkenee. Kun oksan kärki on kasvaessaan tarpeeksi etääntynyt lähimmästä haarasta, tietylle etäisyydelle siitä syntyy uusi haara.
On ehdotettu, että tämä järjestelmä aiheuttaisi myös haarojen spiraalisen asettumisen, kun olemassa olevien haarojen tuottama inhibiittori jakautuisi epätasaisesti varren pintasolukon eri puolille. Tämä johtaisi kuitenkin korkeintaan vuorotellen varren kummallekin puolelle syntyviin tai vastakkain asettuviin lehtiin, jotka vuorottelevat 90° kulmassa, sillä alemmat lehdet sijaitsevat niin kaukana, että ne vaikuttavat lehden syntyalueeseen vain vähän. Onkin havaittu, että spiraalista fyllotaksiaa ilmentävissä kasveissa esiintyy lisäksi toista, paljon hitaammin diffusoituvaa inhibiittorihormonia, joka toimii kasvupisteen ympäristössä eräänlaisena muistijälkenä siitä, mihin suuntaan aikaisemmat lehdet ovat syntyneet. Lehden sijoittumiseen vaakasuunnassa vaikuttaa siis eri hormoni kuin pystysuunnassa. Tämäkin hormoni laimenee pikkuhiljaa, jolloin vanhempien lehtien vaikutus sen konsentraatioon vähenee. [13]
Mykerön fyllotaksiaan tämä teoria ei sovellu. Mm. havainto, että mykerön keskiosan leikkaaminen pois ei vaikuta fyllotaksian syntyyn kumosi aikaisemmat teoriat keskipisteen erittämästä hormonista. On myös ongelmallista, että kukat syntyvät ensiksi mykerön reunoille, mutta osaavat silti muodostaa oikean määrän spiraaleita.
Erään teorian mukaan kukkien sijoittuminen määräytyy fyysisen kosketuksen mukaan [1, 2, 3, 4, 10]. Uusi kukan alku syntyy minne tahansa, missä olemassa olevien kukkien väliin jää tarpeeksi tilaa. Kukat työntävät toisiaan, ja pyrkivät siirtymään mahdollisimman etäälle muista kukista. Tällöin kukkienjärjestys voi muuttua kehityksen myöhemmässäkin vaiheessa, etkä niiden täydy heti aluksi löytää lopullista paikkaansa.
Toisen teorian mukaan kukkien asettuminen määräytyisi kemiallisesti, kuten edellä mainitussa teoriassa lehtien syntymisestä. Kukkakuvion muodostukseen osallistuu kuitenkin sekä aktivaattori että inhibiittori, jotka vaikuttavat paitsi kukkien syntyyn, myös toistensa tuotantoon soluissa. Hormonit päätyvät lopulta tasapainotilaan, joka määrää kukkien syntypaikat. [10, 18] Tietokonesimulaatioissa tämä malli johtaa vastaaviin kuvioihin, kuin kosketusmallinkin, joten tällä perusteella on vaikea sanoa kumpi on lähempänä totuutta.
[1] Adler, Irving; A Model of Contact Pressure in Phyllotaxis. Journal of Theoretical Biology 45:1–79 (1974)
[2] Adler, Irving; A Model of Space Filling in Phyllotaxis. Journal of Theoretical Biology 53:435–444 (1975)
[3] Adler, Irving; The Consequenses of Contact Pressure in Phyllotaxis. Journal of Theoretical Biology 65:29–77 (1977)
[4] Fowler, Deborah R.; Prusinkiewicz, Premyslaw; Battjes, Johannes; A Collision.based Model of Spiral Phyllotaxis. Computer Graphics, 26, 2 (1992)
[5] Haß, Helmut (2000); Phyllotaxis Phänomen und Modellierung lebendiger Ordnung. http://www.uni-koblenz.de/~odsgroe/wwwha/spiralen/www-phyllotaxis/0.phyllotaxis.html
[5] Hotton, Scott G. (2000) Scott Hotton's Phyllotaxis Page, http://unixgen1.mcs.muohio.edu/~hottonsg/phyllo.html
[6] Hotton, Scott G.; Symmetry of Plants. University of California, Santa Cruz, 1999.
[7] Smith College, Phyllotaxis – an Interactive Site for Mathematical Study of Plant Pattern Formation, http://www.math.smith.edu/~phyllo/
[8] Thomas, R. L.; Cannell, M. G. R.; The Generative Spiral in Phyllotaxis Theory. Annals of Botany 45:273–249 (1980).
[9] Jean, Roger V.; Mathematical modelling in Phyllotaxis: The State of the Art. Mathematical Biosciences 64:1–27 (1983)
[10] Jean, Roger V.; Phyllotaxis – A Systemic Stydy in Plant Morphogenesis. Cambridge University Press, 1994.
[11] Maxymowych, R.; Erickson, R. O.; Phyllotactic change induced by by gibberelic acid on Xanthium Shoot Apices. American Journal of Botany 64:33–44 (1977).
[12] Mitchison, G. J.; Phyllotaxis and the Fibonacci Series. Science196:270–275 (1997).
[13] Nill, Karl-Heinz; (2000) Phyllotaxis Helical arrangement of leaves and staggered. http://www.eb.tuebingen.mpg.de/abt.4/meinhardt/phyllo.html
[14] Prusinkiewicz, Premyslaw; Lindenmayer, Aristid; The Algorithmic Beauty ofPlants. Springer-Verlag, New York 1990.
[15] Ridley, J. N.; Packing Efficiency in Sunflower Heads. Mathematical Biosciences 58:129–139 (1982).
[16] Vogel, Helmut; A Better Way to Construct a Sunflower Head. Mathematical Biosciences 44:179–189 (1979)
[17] Weise, Dmitriy (1998) Principle of Minimax and Rise Phyllotaxis (Mechanistic Phyllotaxis Model), http://members.tripod.com/vismath/dima/
[18] Young, David A.; On the Diffusion Theory of Phyllotaxis. Journal of Theoretical Biology 71:421–432 (1978)