Karttuenn, Einar; Kryptologia. Seepia 1 (1999):28-31

Kryptologia

Kryptologia on tiede, joka tutkii salakirjoitusmenetelmiä eli kryptografiaa ja niiden purkamista eli kryptoanalyysiä. Salakirjoitus on sinänsä vanha taito, mutta sen kehitys ja merkitys ovat muuttuneet rajusti sähköisen viestinnän synnyn myötä.

Yksinkertaisimpia salakirjoitusmetodeja ovat ns. korvausmenetelmät kuten muun muassa Julius Caesarin käyttämä nk. Caesar-koodi. Siinä siirretään jokaista aakkosten kirjainta kaksi paikkaa eteenpäin eli a:sta tulee c, l:stä n, q:sta s ja z:sta b käyttäen 26-kirjaimisia aakkosia. Salaus on kuitenkin helppo purkaa, kuten seuraava esimerkki osoittaa: Ecguct-mqqfk.

Toinen samanlainen järjestelmä on ROT13, joka toimii samalla tavalla kuin Caesar-koodi, mutta kirjaimia siirretään 13 paikkaa eteenpäin. ROT13:a käytetään nykyään esim. Usenetissä piilottamaan informaatio, jota kaikki eivät halua nähdä.

Korvaussysteemien purku on hyvin yksinkertaista. Jos se noudattaa yllä olevaa muotoa, on mille tahansa salaiselle tekstille [aakkosten lukumäärä - 1] purkuvaihtoehtoa. Niistä yleensä vain yksi täyttää kielen asettamat vaatimukset. Koodin murtamiseen ei käytännössä kulu paria sekuntia kauempaa nykytietokoneilla. Jos korvaus tehdään sellaisen taulukon mukaan, jossa jokaista kirjainta vastaa sattumanvarainen toinen kirjain, voidaan kirjainten yleisyydestä ja sijainneista ratkaista algoritmi nopeasti. Salauksien purkamisessa on kuitenkin ensiarvoisen tärkeää salatun materiaalin määrä: mitä enemmän sitä on, sitä helpompaa purkaminen on.

Kryptografialla on nykyään kaksi pääsuuntausta: julkisen ja salaisen avaimen kryptografia.

Salaisen avaimen kryptografia

Salaisen eli symmetrisen avaimen kryptografiassa sekä lähettäjällä että vastaanottajalla on sama avain, jolla viesti sekä salakirjoitetaan että puretaan. Tämä kryptografian muoto on perinteinen ja tarjoaa vahvan suojauksen purkuyrityksiä vastaan. Kuitenkin mm. avainten toimitus luotettavasti molemmille osapuolille voi aiheuttaa ongelmia. Salaisen avaimen kryptografiasta on kaksi pääsovellusta: sarja- ja lohkokoodausmenetelmät (engl. stream ja block).

Lohkokoodausmenetelmät

Lohkomenetelmässä (engl. Block cipher) koodataan tietoa aina vakiopituisissa palasissa (nykyään 64 bittiä). Lähes aina käytetään nk. toistavia menetelmiä, joissa sama salaus toistetaan useita kertoja erilaisilla ala-avaimilla. Nämä on johdettu käyttäjän salaisesta avaimesta. Näin salauksen tulos paranee.

Feistelin menetelmä on toistavan menetelmän erikoistapaus, jossa käytetään koko ajan samaa muunnosta. Siinä lähdeteksti jaetaan ensin kahteen osaan a ja b. Tämän jälkeen b käsitellään siten, että sen ja ala-avaimella E_k salatun ensimmäisen puolikkaan (eli E_k(a):n) välillä suoritetaan xor-operaatio (kts. tietoruutu). Alkuperäinen b korvataan näin muunnetulla b:llä ja a jää ennalleen. Seuraavalla kierroksella a muuttuu ja b jää vastaavasti ennalleen. Näin tehdään jokaisella toistokerralla paitsi viimeisellä, jolla tekstin osien järjestystä ei vaihdeta. Feistelin menetelmän hyvä puoli on, että se voidaan purkaa toistamalla samat toimenpiteet kuin pakatessa päinvastaisessa järjestyksessä. Tämä tosin onnistuu myös joillakin muilla ei-Feistel-pohjaisilla lohkokoodatuilla kryptausjärjestelmillä (esim. IDEA).

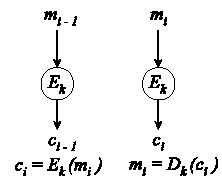
	Lohkomenetelmän funktioilla voidaan koodata monin tavoin dataa, ja näitä erilaisia tapoja kutsutaan yleensä lohkomenetelmän moodeiksi. ECB (Electronic Code Book) on moodeista yksinkertaisin: siinä suoritetaan sama salausfunktio jokaiselle lähdetekstin lohkolle:
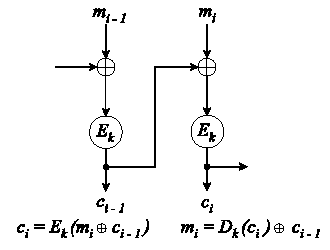
	CBC (Cipher Block Chaining Mode) muistuttaa muutoin EBC-moodia, mutta lähdetekstilohkolle suoritetaan aina ennen salausta xor-operaatio edellisen salatun lohkon kanssa. CBC:ssä virheet monistuvat, mutta viestissä on hyvin vaikea havaita mitään säännönmukaisuuksia:
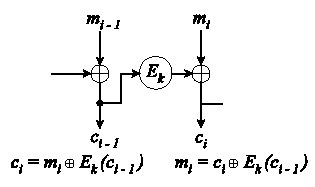
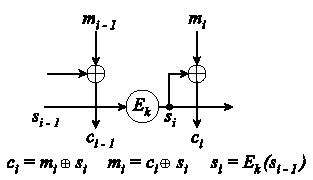
	CFB:ssä (Cipher Feedback Mode) taas lähdetekstille suoritetaan xor- operaatio edellisestä salatusta tekstistä jollain operaatiolla saatavan tekstin kanssa. CFB-moodissa kryptatusta tekstistä näkee alkuperäisen tekstin rakennetta, ja säännömukaisuuksia voi havaita:
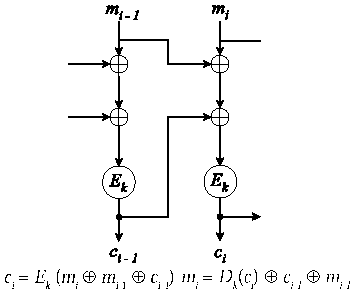
	OFB eroaa CFB:stä siten, että xor-operaation toista operandia ei saada vanhasta lähdetekstistä, vaan se lasketaan erikseen (kaaviossa se on s, joka voi ensimmäisellä salauskierroksella olla jokin sovittu vakio, esim. 3). OFB (Output Feedback Mode) eroaa CFB:stä edukseen siinä, etteivät virheet leviä. Toisaalta salattua dataa on helpohko muuttaa, koska yhden salatun viestin kohdan muuttaminen ei vaikuta koko viestin muutoksenjälkeiseen osaan, toisin kuin CFB:ssä:
	Lisäksi on muita vähemmän yleisessä käytössä olevia moodeja kuten PCBC, jonka tarkoitus on monistaa mahdollista virhettä ja näin helpottaa dataan syntyneiden virheiden havaitsemista:

Sarjakoodausmenetelmät

Sarjakoodausmenetelmät (Stream cipher) käsittelevät yksittäisiä merkkejä tai useimmiten bittejä eivätkä suurempia kokonaisuuksia kuten lohkokoodausmenetelmät. Toisin kuin lohkomenetelmällä koodautuvat lähdetekstin osat eri tavalla siitä riippuen, missä kohtaa lähdetekstiä ne sijaitsevat. Eräs sarjamenetelmän hyviä puolia on, ettei se monista virheitä, vaan ainoastaan vaurioitunut osa purkautuu väärin. Mikään sarjamenetelmä ei ole noussut standardin asemaan, mutta niistä ehkä suosituin on RC4. Vaikka sarjamenetelmiä käytetäänkin runsaahkosti etenkin kiinteissä ratkaisuissa (eli kun salauksen ja purkamisen suorittaa erityisesti sitä varten rakennettu laite), on niitä käyttäviä algoritmejä julkaistu vähemmän kuin lohkomenetelmään perustuvia algoritmejä.

Salaus perustuu useimmiten avaimen ja lähdetekstin xor- operaatioon. Jos sisällöltään satunnainen avain on pitempi kuin viesti, on viestiä mahdoton murtaa. Tätä kutsutaan kertakäyttö- (one-time pod) tai Verdan menetelmäksi. Sillä on kuitenkin useita huonoja puolia kuten avaimen kertakäyttöisyys. Avaimien pituuden ja kertakäyttöisyyden vuoksi Verdan menetelmää ei sovelleta käytäntöön sellaisenaan. Nykyiset sarjamenetelmät perustuvatkin lyhyempiin avaimiin, joista lasketaan pitempiä lähes satunnaisia avaimia. Näillä suoritetaan xor- tai muu salausoperaatio. Pitkien avainten muodostamiseen käytetään usein LFSR:iä (Linear Feedback Shift Register)

esimerkki-LFSR:

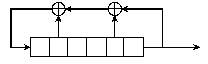
(Laatikot ovat avaimen bittejä, siis ykkösiä tai nollia; syntyvään avaimeen liitettävä bitti tulee ulos oikeassa reunassa.)

Avainta siirretään aina yhden bitin verran oikealle ja ylijäävä bitti liitetään uuteen avaimeen. Vasemmanpuolimmaiseen bittiin siirretään valituista biteistä xor:n arvo. Esim. kuvassa ensin suoritetaan xor toiselle ja uuteen avaimeen liitetylle bitille. Seuraavaksi tuloksella suoritetaan xor-operaatio viidennen bitin kanssa ja tulos sijoitetaan vasemmanpuoleisimpaan bittiin. LFSR:n alkuarvo on yleensä alkuperäinen salainen avain.

LFSR ei kuitenkaan yksinään tuota riittävää turvallisuutta, joten siihen perustuvia ratkaisuja on kehitelty edelleen. Ratkaisuna on ollut mm. ”shift register cascade”:t, joissa on useita LFSR:iä, jotka ohjaavat toisiaan esim. siirtymään kaksi askelta oikealle yhden sijaan. Eräs parhaimmista ratkaisuista on ollut ns. ”shrinking generator”, jossa yksi LFSR päättää, käytetäänkö toisen tulosta uuden avaimen osana vai ei. Se on osoittautunut hyvin luotettavaksi, vaikkakin siinä on ongelmana, ettei avain synny tasaisella nopeudella. Sarjamenetelmää käytetään useimmin kiinteissä ratkaisuissa eikä niinkään paljon ohjelmistoissa.

Julkisen avaimen salausmenetelmät

Julkisen avaimen eli asymmetrinen salaus on toinen salauksen päämuoto. Siinä käytetään kahta avainta, toista julkista viestien koodaamiseen ja toista salaista salauksen purkamiseen. Tämän salaustavan etuna on avaimen levitettävyys: sen salaamiseen ei ole mitään tarvetta. Huonoja puolia ovat salauksen hitaus ja turvallisten avainten pituus. Julkisen avaimen salaus on suhteellisen uusi menetelmä: se kehitettiin 1976. Sitä voidaan käyttää paitsi varsinaiseen salaukseen myös lähettäjän varmennukseen kuten sähköiseen allekirjoitukseen.

Julkisen avaimen kryptografia perustuu ns. vaikeisiin ongelmiin (Hard Problems), jollaisena pidetään esim. suurten kokonaislukujen tekijöihinjakamisongelmia. Kryptografiaa koskettavat ongelmat voidaan jakaa kahteen luokkaan: niihin, jotka voidaan ratkaista rajoitetussa ajassa (P) ja niihin, joita nykykäsityksen mukaan ei voida ratkaista rajoitetulla aikavälillä (NP). Kaikki joukon P ongelmat kuuluvat myös joukkoon NP, mutta ei tiedetä, kuuluvatko kaikki joukon NP-ongelmat joukkoon P. NP-täydellisiksi (NP-complete) kutsutaan ongelmia, jotka voidaan muuttaa miksi tahansa toiseksi NP-täydelliseksi ongelmaksi rajallisessa ajassa. Jos siis mikä tahansa NP-täydellinen ongelma ratkaistaisiin niin, olisi ratkaistu kaikki NP-täydelliset ongelmat. Kuitenkin nykyään ollaan sitä mieltä että P¹NP.

Yhtenä yleisimmistä vaikeana ongelmana pidettävistä ongelmista on suurten lukujen tekijöihin jako, joka on tietokoneelle hidasta ja monimutkaista. Toinen vaikeana pidetty ongelma liittyy diskreetteihin logaritmeihin. Se perustuu vaikeisiin sarjoille suoritettaviin laskutoimituksiin.

Menetelmien etuja ja haittoja

Symmetrinen avain siis tarjoaa huomattavasti nopeamman salauksen kuin asymmetrinen. Yhtä vaikeasti murrettaviin viesteihin joudutaan käyttämään usein kymmenen kertaa pidempiä julkisia avaimia kuin symmetrisiä. Julkinen avain taas tarjoaa mahdollisuuden mm. sähköisiin allekirjoituksiin. Julkisen avaimen suurin hyöty on kuitenkin avainten levityksen ongelmattomuus. Niinpä symmetrinen salaus onkin ehdottomasti parempi suljetuissa järjestelmissä kuten vaikka pankin sisäisessä atk-järjestelmässä tai kotitietokoneen tiedostojen salauksessa. Kuitenkin esim. sähköposteissa on julkisen avaimen salauksilla kuten pgp:llä selvät etunsa nimenomaan niiden vähäisistä avainongelmista johtuen. Symmetrisiä salausratkaisuja voidaan helposti yhdistellä. Ne ovat vanhempia ja niiden matemaattinen tausta tunnetaan paremmin. Vaikka avaimet saataisiinkin vaihdettua turvallisesti, luo kuitenkin tarve vaihtaa avaimia säännöllisesti lisää avainongelmia. Julkisen avaimen kryptografiassa taas tarvetta avaimen vaihtoon ei ole kovinkaan usein. Julkisen avaimen salauksella on lisäksi paljon paremmat sovellusmahdollisuudet sähköisessa allekirjoituksessa; symmetrisellä salauksella toteutettuna siinä pitäisi käyttää paljon pitempiä avaimia. Julkisten salausten ongelmana on kuitenkin niiden uutuus ja se, ettei niiden turvallisuutta ole todistettu matemaattisesti.

Hash-funktiot

Kryptografiaan käytettävien hash-funktioiden h(x)=c täytyy täyttää viisi edellytystä. Niiden pitää hyväksyä miten pitkä argumentti tahansa ja palauttaa vakiomittainen arvo. Lisäksi h(x):n pitää olla helpohko laskea kaikilla x:n arvoilla. Funktioiden pitäisi olla yksisuuntaisia eli vaikka h() ja c tunnettaisiinkin, ei x:ää pitäisi pystyä selvittämään ainakaan helposti. Sille pitäisi olla aina voimassa ehto: jos tunnetaan viesti x, ei ole mahdollista laskea y:tä jolle olisi voimassa h(x)=h(y), kun x ¹y eli funktio ei saa samaa arvoa kahdella eri argumentin arvolla. Hash-funktioita käytetään ehkä eniten sähköisiin allekirjoituksiin ja datan eheyden varmistamiseen (esim. funktio crc-32).

Kryptoanalyysi

Kryptologiaan kuuluu kiinteästi kryptoanalyysi, jolla mm. eri salausmetodien turvallisuutta testataan. Yksinkertaisin kryptoanalyysimenetelmä on ns. brute-force-hyökkäys, jossa käydään läpi kaikki mahdolliset avaimet. Tämä on kuitenkin hyvin hidasta, koska esim DES:ssä on 2⁵⁶ avainta. On kuitenkin kehitetty erilaisia menetelmiä, joilla saadaan laskentatarvetta pienennettyä tutkimalla esim. miten kaksi toisiaan läheisesti muistuttavaa lähdetekstiä koodautuvat tai yrittämällä löytää säännöllisyyksiä, joiden kautta paloja avaimesta saadaan murrettua.

Kryptologian asema tulee päivä päivältä tärkeämmäksi erilaisten sähköisten viestintämetodien suosion kasvaessa. Esimerkiksi sähköisen kaupankäynnin perusedellytyksiin kuuluu turvallinen kryptografia, jolla asiakas tunnistetaan ja tietoja kuten luottokortin numeroita siirretään verkossa. Myös sähköisen viestinnän yksityisyyden turvaamisessa on kryptografia omiaan kuten suosittu pgp-salausmenetelmä osoittaakin. Kryptologiaa käsitteleviä kirjoja ei ole julkaistu suomeksi juurikaan, mutta englanninkielisiä teoksia löytyy jonkin verran. Kirjallisuutta on vaikeahko löytää Suomesta. Tietojenkäsittelytieteen laitoksella on alaa käsittelevää kirjallisuutta, mutta lainausoikeus on vain laitoksen opiskelijoilla. Kirjoja saa kuitenkin lainaan TKK:n kirjastosta. Aiheesta eniten ajankohtaista tietoa löytyy kuitenkin Internetistä.

Einar Karttunen

Eri Salausmenetelmiä

RSA

RSA on laajimmalle levinnyt julkisen avaimen salaus. Sen kehittivät R. Rivest, A. Shamir, and L. Adleman, joiden mukaan se nimettiinkin, vuonna 1977. RSA:ta käytetään paitsi tiedon salaamisessa myös sähköisissä allekirjoituksissa. Se perustuu suurten kokonaislukujen tekijöihinjaon vaikeuteen. RSA:n avain muodostetaan seuraavalla tavalla: Valitaan kaksi suurta alkulukua p ja q ja lasketaan niiden tulo n, jota kutsutaan myös modulukseksi. Valitaan luku e, joka täyttää ehdot e<n ja jolla ei ole yhteisiä tekijöitä (p-1)(q-1) kanssa. Valitaan toinen luku d siten, että (de-1)mod((p-1)(q-1))=0. Julkinen avain muodostuu lukuparista (n,e) ja salainen parista (n,d). Turvallisuus perustuu siis vaikeuteen laskea e:stä d. RSA:lla koodaus on hidasta, ohjelmallisesti noin 100 kertaa ja kiinteällä laitteistolla 1000-10000 kertaa hitaampaa kuin DES-koodaus. Turvallisena pidetyn avaimen pituus on vuosien varrella kasvanut, nykyään yleistä 512 bitin avainta pidetään turvattomana ja suositellaankin käytettävän pitempiä 768, 1024, tai jopa 2048 bitin avaimia. Toisaalta avaimen kasvanut koko hidastaa kryptausta ja sen purkua huomattavasti. Avaimen pituuden kaksinkertaistuessa nelinkertaistuu salaukseen ja sähköisen allekirjoituksen varmentamiseen kuluva aika. Purkamiseen ja sähköisen allekirjoituksen tekoon kuluva aika kahdeksankertaiskuu, ja uuden avaimen laskentaan kuluva aika 16-kertaistuu. Yksi hyvä RSA:n käyttökohde on kryptausjärjestelmien hyvien puolien yhdistäminen. Voidaan ensin esim. salata viesti satunnaisella IDEA(eräs symmetrinen salausjärjestelmä)-avaimella, salata sitten tämä avain vastaanottajan julkisella RSA-avaimella ja lähettää viesti, joka koostuu IDEA:lla salatusta datasta ja RSA:lla salatusta avaimesta. Näin saavutetaan toisaalta nopea purettavuus ja toisaalta parempi turvallisuus.

DES

DES eli ”Data Encryption Standard” on yksi vanhimpia yleisessä käytössä olevia salausjärjestelmiä. Sen kehittivät pääasiassa IBM ja NSA, minkä vuoksi monet ovatkin epäilleet sitä tarkoituksella heikennettäneen. DES perustuu symmetriseen lohkosalaukseen. Se käyttää 64 bitin lohkoja ja 56 bitin avainta. DES-salaus perustuu 16-kertaiseen Feistel-koodausmenetelmään jossa moodia voidaan vaihdella. Salausta pidetään turvattomana sen avaimen lyhyyden vuoksi. Nykyään kuitenkin käytetään usein kolminkertaista DES-salausta, joka tarjoaa paremman tietoturvan kuin alkuperäinen.

Elliptiset käyrät

Elliptisiin käyriin pohjautuvat salausjärjestelmät ovat uudehko keksintö: ne kehitettiin 80-luvun puolivälissä. Käyrät seuraavat muotoa y² = x³ + ax + b. Näiden avulla tiedon salaus vastaa julkisen avaimen salausta, jossa aritmeettiset laskutoimitukset on korvattu elliptisiin käyriin liittyvillä ongelmilla, joiden uskotaan olevan em. vaikeita ongelmia. Salauksella on kaksi pääsuuntaa. RSA:ta muistuttavat metodit muodostavat toisen pääsuuntauksen, joka ei tarjoa paljoakaan etuja verrattuna alkuperäiseen RSA:han.

Toinen, lupaavampi suuntaus perustuu diskreettien logaritmien (discrete logarithm) ongelmaan. Se perustuu siihen, että valitaan käyrältä kaksi pistettä Y ja G, niin että Y=kG. Menetelmä perustuu kokonaisluku k:n löytämisen vaikeuteen.

Kirjallisuutta

[1] Menezes, A.; van Oorschot, P.; Vanstone, S.; Handbook of Applied Cryptography. CRC Press, 1996

[2] RSA Laboratories’; Frequently Asked Questions About Today’s Cryptography, v4.0;
www.rsasecurity.com/rsalabs/faq/.

[3] Attacks against the BEST encryption algorithm — Chaos is definitely not randomness, Written by +Spath:
129.105.116.5/fravia/best0001.htm.